AREA OF A CIRCLE-In SAVAN's approach


Here is a way to find the formula for the area of a circle:


Cut a circle into equal sectors (12 in this example) 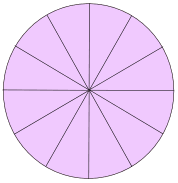circle 12 sectors

Divide just one of the sectors into two equal parts. We now have thirteen sectors – number them 1 to 13:

circle 13 including 2 half slices

Here Area of sector1=Area of sector13=1/2*Area of sector2.

Rearrange the 13 sectors like this:

sectors laid out like rectangle

Which resembles a rectangle:

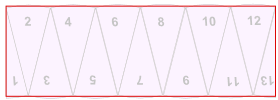
sectors with rectangle on top

What are the (approximate) height and width of the rectangle?

The height is the circle's radius: just look at sectors 1 and 13 above. When they were in the circle they were "radius" high.

     sectors laid out like rectangle 

Note that Here length of the approximated rectangle is bumpy edges of 6 sectors. And initially, we divided the circumference of the circle( 2 × π × radius)equally into 12 sectors.

The width (actually one "bumpy" edge) is half of the curved parts around the circle ;which are shared equally at both sides(length sides)... in other words, it is about half the circumference of the circle.

We know that:

                       Circumference = 2 × π × radius:

And so the width is about:

                        Half the Circumference = π × radius

And so we have (approximately):

rectangle is (pi x radius) by radiusradius
π × radius 

Now we just multiply the width by the height to find the area of the rectangle:

Area = (π × radius) × (radius)

= π × radius2

Note: The rectangle and the "bumpy edged shape" made by the sectors are not an exact match.

But we could get a better result if we divided the circle into 25 sectors (23 with an angle of 15° and 2 with an angle of 7.5°).

And the more we divided the circle up, the closer we get to be exactly right.

Conclusion:

                                    Area of Circle = π r2 


 

Comments

Post a Comment

popular

Lockdown is the world's biggest psychological experiment - and we will pay the price

Image
How India's lockdown has affected mental health- A special article on combating Covid-19 What will the psychological impact be for 2.6 billion people under lockdown? India’s public landscape has transformed dramatically over the last couple of months, with the most prolonged lockdown that the present generation can remember. Declared on March 24, 2020, the lockdown ensured that hundreds of millions of people were effectively confined to home, except when they ventured out, armed with a self-attested affidavit, to stock up on essentials. While this may have been effective in helping to curb the spread of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in India, it has not, perhaps, been conducive to the emotional and mental health of some groups. A recent study published on the preprint server  medRxiv *  in May 2020 concludes that select groups might have suffered emotionally, and outlines measures to alleviate such potential harm. 14 ways to protect your ment...
Read more

What would happen if Earth started to spin faster!?.......?

Image
What would happen if Earth started to spin faster? Even a 1 mph speed boost would make things pretty weird               Things would get pretty catastrophic. There are enough things in this life to worry about. Like  nuclear war ,  climate change , and  whether or not you're brushing your teeth correctly . The Earth spinning too fast should not be high up on your list, simply because it's not very likely to happen anytime soon—and if it does, you'll probably be too dead to worry about it. Nevertheless, we talked to some experts to see how it would all go down. First, let’s talk about how fast the world is spinning now. That actually depends on where you are, because the planet spins fastest around its waistline. As Earth twirls around its axis, its circumference is widest at the equator. So a spot on the equator has to travel a lot farther in 24 hours to loop around to its starting position than, say, Chicago, which sits on a narrower c...
Read more

PYTHAGOREAN Theorem-In SAVAN's approach

Image
What is the Pythagorean Theorem? You can learn all about the  Pythagorean Theorem , but here is a quick summary: The Pythagorean Theorem says that,  in a right triangle,  the square of a (a 2 ) plus the square of b (b 2 ) is equal to the square of c (c 2 ): a 2  + b 2  = c 2 Proof of the Pythagorean Theorem using Algebra We can show that  a 2  + b 2  = c 2  using  Algebra Take a look at this diagram ... it has that "abc" triangle in it (four of them actually):                       Area of Whole Square It is a big square, with each side having a length of  a+b , so the  total area  is: A = (a+b)(a+b)              ...(1) Area of The Pieces Now let's add up the areas of all the smaller pieces:    First, the smaller (tilted) square has an area of: c 2     Each of the four triangles has an area of:(1/2)*ab=ab/2 So all ...
Read more

Indian Gamers Enjoy 'Chicken Dinner' as PUBG Escapes Chinese App Ban List

Image
Chinese Apps Banned In India:  Chinese Media Express Shock Over Blocking Of Apps By Indian Government The Indian government has banned a total of 59 Chinese apps including the teen favourite TikTok.  The biggest news trending is that Chinese Apps have been banned in India. The Chinese apps have been blocked by the Indian government after the deadly clash between Indian and Chinese soldiers along the contested border which left 20 Indian soldiers dead.  The Indian ministry called the Chinese-owned applications as “prejudicial to sovereignty and integrity of India, defence of India, the security of the state and public order.”  The Indian Cyber Crime Coordinate Centre under the Ministry of Home Affairs sent an exhaustive recommendation for blocking these “malicious apps”. The ministry said that it has “received many complaints from various sources including several reports about the misuse of some mobile apps available on Android and iOS platforms for stealing and surr...
Read more

(a + b) (a - b)= a² - b² -In SAVAN's approach

Image
Geometric Proof of the Difference of Squares: a² - b² The  difference of two squares  is subtracting a square number from another squared number. And these numbers don’t have to be perfect squares. Thankfully, the difference of squares can be factored easily. a² - b²  is ubiquitous in mathematics and it is also supercalifragilisticexpialidocious for algebra. If we speak algebraically: (a + b) (a - b) = a² + ba - ab -b² = a² - b² But there is a different and beautiful way to represent  a² - b² . We can create multiple representations of this single concept. This is the beauty of mathematics. For instance, geometric objects are so powerful to visualize algebraic formulas and equations. Let’s think about it geometrically a little bit. This blue shape below has an area of  a² - b² . And we can reveal an algebraic identity by  rearranging.          To do this, first, we make a cut and split the shape into two different rectangles; the bl...
Read more